Эта переменная не определена mathcad ошибка матрицы

MathCad | ANSYS CFX | MS Office

Поиск по сайту

Выбор языка

Часто в курсовом проекте, либо в лабораторной работе встает вопрос о решении какого-либо сложного большого уравнения с одним неизвестным. Не всегда хочется тратить 10 — 20 минут на рутинные преобразования в процессе которых, велика вероятность допущения ошибки. Целесообразно воспользоваться математической программой (в данном случае MathCad), которая быстро и правильно сможет дать ответ. Мы рассмотрим пример использования 2-ух способов решения уравнений, причем как в числах так и в символьном виде.

Способ №1: использование вычислительного блока Given — Find:

Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем первое слово Given. Это служебное слово. Оно «подключает» определенные программные модули mathcad, необходимые для решения уравнения. Эти модули в своем составе содержат основные численные методы решения: метод бисекции, простой итерации и пр. Далее пишется наше уравнение в любом — явном или неявном виде. Само уравнение набирается с клавиатуры с использованием логического символа «равно». На панельке Boolean (Булева алгебра) он выделен жирным шрифтом (см. рис. 1).
Рис. 1. Панель «Булевая алгебра»
Далее пишется слово Find(x) (где х — переменная). Это функция, которая и получает ответ. Функцию Find(x) можно присвоить какой-либо переменной и использовать далее в расчетах. Для получения результата, после Find(x) следует поставить символ «→» либо «=» (см. рис. 2).
Рис. 2. Панель «Вычисления»
В зависимости от сложности уравнения через некоторое время MathCad выведет результат.

Возможности MathCad позволяют определить корень как в численном виде (т. е. результат решения уравнения представляет собой число) так и в символьном (результат — выражение). Для численного определения корня необходимо задать (определить) ВСЕ переменные входящие в уравнение и даже искомую переменную. MathCad воспринимает задание искомой переменной как начальное приближение корня. Крайне важно задаться начальным приближением, поскольку без него корень уравнения невозможно определить в силу особенностей используемых численных методов. Нужно отметить, что некорректное задание начального приближения часто становится причиной получения неверного результата либо его отсутствия вообще. Но не стоит забывать также и о том, что корня может не быть, потому что само уравнение его не имеет.
В том случае, если необходимо решить уравнение относительно какой-либо переменной в символьном виде, то нет необходимости задаваться значениями всех входящих в уравнение параметров и начальным приближением переменной. В этом случае достаточно ввести уравнение (также через «жирное равно») и после оператора Find(x) поставить «→». При этом будут работать уже другие функции MathCad, которые заточены под символьное преобразование и упрощение выражений. Результатом решения будет выражение. Стоит отметить, что MathCad сможет записать решение далеко не всякого уравнения. В этом смысле его возможности ограничены.

Для подтверждения и закрепления выше сказанного, Вам предлагается скачать и познакомиться с примерами решения уравнений как в численном так и в символьном виде.

Пример №1. Решение уравнения в MathCad с помощью блока Given Find численно: Скачать

Пример №2. Решение уравнения в MathCad с помощью блока Given Find символьно: Скачать

Способ №2: Применение метода solve:

Этот метод по существу не отличается от выше рассмотренного, поскольку процедура нахождения корня аналогична. Разница лишь в оформлении. В этом случае наше уравнение записывается без операторов Given и Find. После ввода уравнения на панели Symbolic нажимаем кнопку solve (см. рис. 3), определяем через запятую искомую переменную, жмем «→» и получаем ответ.
Рис. 3. Панель «Символьные»
Иногда, то что не получается найти с помощью Given Find получается в solve.

Пример №3. Решение уравнения в MathCad с помощью solve: Скачать

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

• отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
• уточнение корней – нахождение численного значения корня с указанной точностью.

Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

• f(x) – функция левой части уравнения f(x) = 0;
• x – переменная, относительно которой требуется решить уравнение;
• a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде

Этот прием используется в Mathcad так:

1. задается матрица коэффициентов при неизвестных системы A;
2. задается столбец свободных членов b;
3. вводится формула для нахождения решения системы X:=A -1 b;
4. выводится вектор решений системы X=.

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

1. Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
2. Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
3. Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

1. В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
2. Выполнить задание 1.

Задание 1. Решить уравнение .

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

После указанных преобразований график функции f(x) будет выглядеть следующим образом:

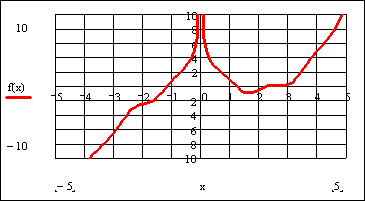
Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

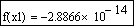
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

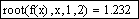
Задание 2. Решить уравнение .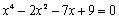

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

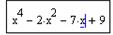
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

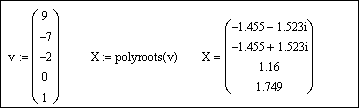
Задание 3. Решить систему линейных уравнений 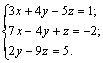Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

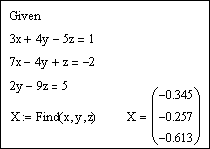
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

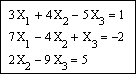
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

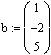
Решим систему матричным способом по формуле

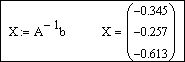
Решим систему с помощью функции lsolve:

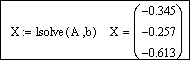
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

программирование mathcad скалярный трехмерный

Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given — Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.

Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given — Find:

— задать начальное приближение

— ввести служебное слово

• — записать уравнение, используя знак боулево равно
• — написать функцию find с неизвестной переменной в качестве параметра

В результате после знака равно выведется найденный корень.

Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.

В Mathcad можно писать программы двух видов

• 1)в виде скриптов(последовательность команд)
• 2)в виде настоящих программ с входными и выходными параметрами.

Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.

Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT).

Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.

Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).

Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.

Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).

Программа содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.